Zobecněný Cam clay model (GCC)
Tento model představuje podstatné vylepšení Modifikovaného Cam clay (MCC) modelu, zejména při modelování zeminy v nadkritické oblasti (supercritical domain), viz obrázek, kde podmínka porušení kopíruje klasické modely typu Mohr-Coulomb, Drucker-Prager a Modifikovaný Mohr-Coulomb (MMC). Na rozdíl od Modifikovaného Cam clay modelu (čárkované linie) má průmět do deviatorové roviny stejný tvar jako Modifikovaný Mohr-Coulombův model. Průmětem MCC modelu je podobně jako v případě Drucker-Pragerova modelu kružnice. V podkritické oblasti (subcritical domain) se modely MCC a GCC chovají identicky. Při odtížení se předpokládá lineární odezva zeminy. GCC model lze použít pouze v případě rozšířených možností programu. Spolehlivá inicializace modelu je popsána v kapitole "Numerická implementace MCC a GCC modelů".
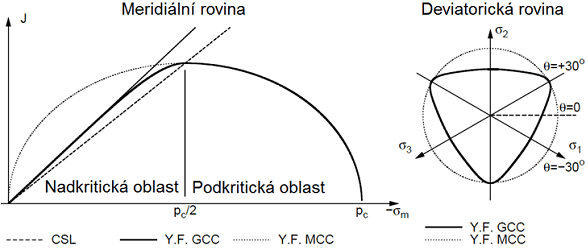 Průmět plochy plasticity MCC a GCC modelu do meridiální a deviátorové roviny
Průmět plochy plasticity MCC a GCC modelu do meridiální a deviátorové roviny
Parametry, které je třeba zadat při použití Zobecněného Cam clay modelu, jsou shodné s parametry modelů MCC a MMC:
κ | - | směrnice linie bobtnání [-] | |
λ | - | směrnice linie normální konsolidace (NCL) [-] | |
e0 | - | počáteční číslo pórovitosti [-] | |
OCR | - | číslo překonsolidace | |
c | - | koheze | |
φ | - | úhel vnitřního tření | |
φcv | - | úhel vnitřního tření při konstantním objemu | |
ν | - | Poissonovo číslo |
Parametry κ a λ lze odhadnout ze vztahů:
![]()
![]()
kde: | Cc | - | součinitel jednoosé stlačitelnosti |
Cs | - | součinitel jednoosého bobtnání |
Tyto parametry lze získat z jednoduché eodemetrické zkoušky.
Podobně jako u MCC modelu je základem formulace GCC modelu vztah mezi číslem pórovitosti (objemovou deformací) a středním efektivním napětím jak je patrné z následujícího obrázku. Oba grafy jsou vázány vztahem:
![]()
![]()
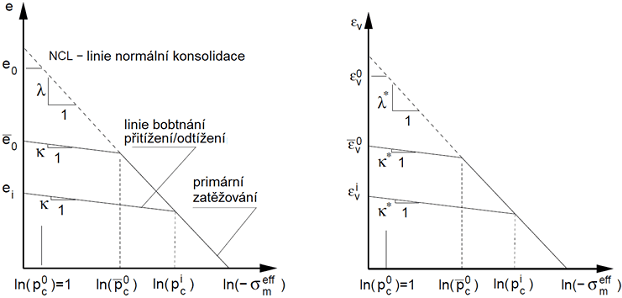 Odezva materiálu při isotropní kompresi (konstitutivní model)
Odezva materiálu při isotropní kompresi (konstitutivní model)
Vývoj podmínky plasticity (zpevnění/změkčení) je řízen aktuálním předkonsolidačním napětím pc:
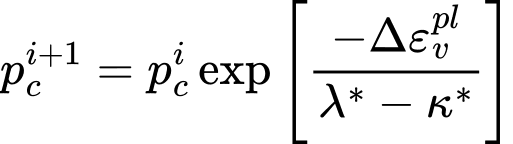
kde: |
| - | aktuální předkonsolidační napětí |
| - | přírůstek objemové plastické def |