Modifikovaný Cam-clay model (MCC)
MCC model byl původně navržen pro popis plastického přetváření jílovitých zemin nacházejících se ve stavu triaxiálové napjatosti. Na základě experimentálních měření byl navržen konstitutivní model vyjadřující změny čísla pórovitosti e (objemovou deformací εv) a logaritmu středního efektivního napětí σmeff, jak je patrné z následujícího obrázku. Oba grafy jsou vázány vztahem:
![]()
![]()
κ | - | směrnice linie bobtnání [-] | |
λ | - | směrnice NCL (linie normální konsolidace) [-] | |
e | - | aktuální číslo pórovitosti [-] |
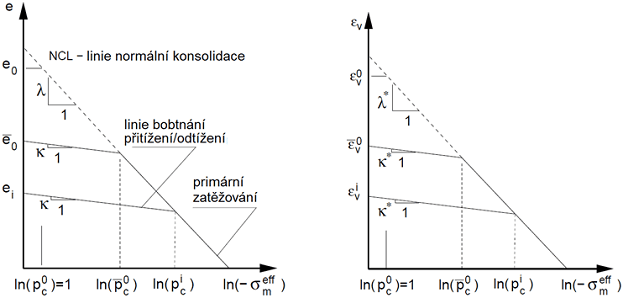 Odezva materiálu při isotropní kompresi (konstitutivní model)
Odezva materiálu při isotropní kompresi (konstitutivní model)
V případě panenské zeminy (virgin soil - normálně konsolidovaná zemina) je chování zeminy dáno tzv. linií normální konsolidace (NCL). Za předpokladu, že zemina již byla zkonsolidována na určitou úroveň danou parametrem pc (předkonsolidační tlak - preconsolidation pressure) a následně odtížena, je chování zeminy při opětovném zatěžování nejprve popsáno tzv. linií bobtnání (odtížení-přitížení). Při opětovném překročení parametru pc je přetvoření opět dáno linií normální konsolidace (primární zatěžování - linie komprese).
Parametry κ a λ lze odhadnout ze vztahů:
![]()
![]()
kde: | Cc | - | součinitel jednoosé stlačitelnosti |
Cs | - | součinitel jednoosého bobtnání |
Tyto parametry lze získat z jednoduché eodemetrické zkoušky.
Jak je patrné z následujícícho obrázku, je plocha plasticity hladká bez možnosti vývoje tahových napětí. MCC model umožňuje, na rozdíl od první skupiny modelů, přímo modelovat deformační zpevnění/změkčení u normálně konsolidovaných nebo překonsolidovaných zemin, nelineární závislost mezi objemovou deformací a středním napětím a limitní podmínky ideální plasticity. Při použití modelu MCC lze zeminu vystavenou smykové deformaci plasticky přetvářet bez kolapsu (body 1,2 pro případ zpevnění, bod 1 pro případ změkčení) až do okamžiku, kdy je dosaženo kritického stavu (bod 3 pro případ zpevnění, bod 2 pro případ změkčení). Zemina se pak dále přetváří pouze smykem bez změny e a σmeff. Při odtížení se předpokládá lineární odezva zeminy.
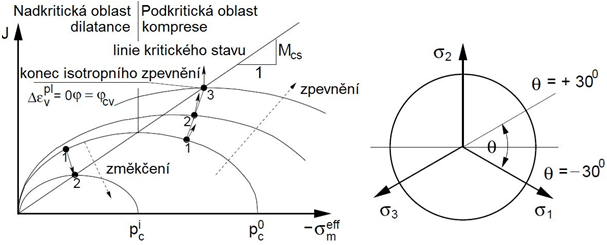 Průmět plochy plasticity do meridiální a deviatorické roviny
Průmět plochy plasticity do meridiální a deviatorické roviny
Vývoj podmínky plasticity (zpevnění/změkčení) je řízen aktuálním předkonsolidačním napětím pc:
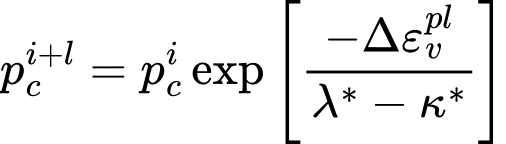
kde: |
| - | aktuální předkonsolidační napětí |
| - | přírůstek objemové plastické deformace |
Vedle parametrů κ, λ, vlastní tíhy a Poissonova čísla vyžaduje MCC model zadání následujících tří parametrů:
Mcs | - | směrnice linie kritického stavu [-] |
e0 | - | počáteční číslo pórovitosti [-] |
OCR | - | součinitel překonsolidace [-] |
Spolehlivá inicializace modelu je popsána v kapitole "Numerická implementace MCC a GCC modelů".
Směrnici kritického stavu Mcs lze určit z výrazu:
| , pro triaxiálovou kompresi |
| , pro triaxiálovou extenzi |
kde φcv je úhel vnitřního tření při konstantním objemu odpovídající kritickému stavu.