Soft soil
Oblast použití Soft soil modelu, původně navrženého v [1], jsou zejména velmi jemné zeminy s vysokým stupněm stlačitelnosti, pro které použití Hardening soil modelu nemusí být vždy vhodné. Podobně jako Hardening soil model tvoří tento model dvě plochy plasticity, smyková ve tvaru Matsuoka-Nakai podmínky porušení a tlaková (compression cap) ve tvaru Zobecněného Cam-clay modelu. V obou případech je tedy průmětem do deviatorické roviny hladká konvexní funkce procházející všemi vrcholy Mohr-Coulombova modelu. Grafické znázornění modelu je na následujícím obrázku.
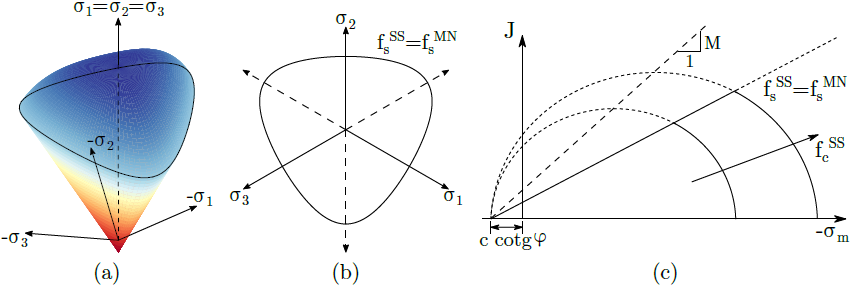 a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
Na rozdíl od Zobecněného Cam-clay modelu je směrnice linie kritického stavu M vyjádřena pomocí součinitele bočního tlaku v klidu normálně konsolidované zeminy K0NC a tuhostních parametrů tlakové podmínky plasticity κ*, λ* blíže specifikované v popisu Modifikovaného Cam-clay modelu, a to ve tvaru
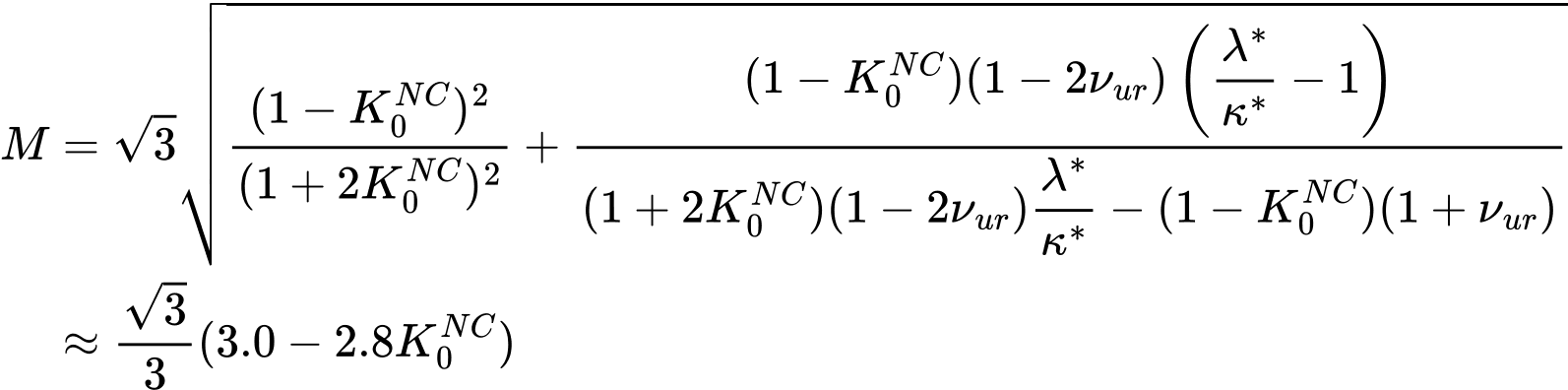
Další informace týkající se parametrů κ*, λ* jsou uvedeny v popisu Modifikovaného Cam-clay modelu. Důvodem zavedení této definice je skutečnost, že hodnota parametru M, která např. v případě Modifikovaného Cam-clay modelu definuje správnou smykovou pevnost, vede k hodnotě K0NC, která významně převyšuje Jákyho výraz pro korektní hodnotu úhlu vnitřního tření φ. Další podrobnosti lze nalézt v [1].
Smyková plocha je definovaná ve smyslu elastického-perfektně plastického materiálového modelu. Tlaková plocha (compression cap) může naopak, na rozdíl od Zobecněného Cam-clay modelu, pouze zpevňovat. Jinými slovy, překonsolidační napětí pc, které řídí vývoj tlakové plochy plasticity, může pouze růst, viz také popis modelu Modifikovaný Cam-clay. Tato skutečnost přináší určitá omezení na volbu parametrů modelu, a to zejména úhlu vnitřního tření φ. Lze ukázat, že zajištění tohoto předpokladu vyžaduje splnění následující podmínky
![]()
Tato podmínka by měla být splněna i v případě, kdy
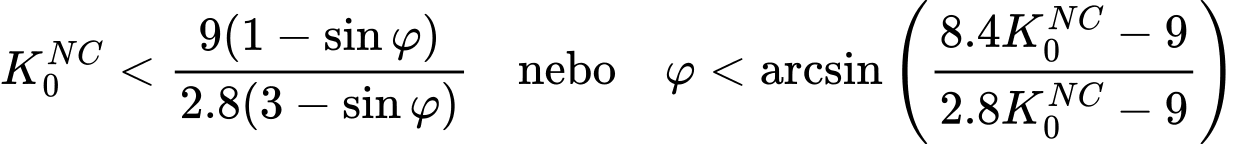
Grafický vztah mezi smykovou a tlakovou podmínkou plasticity je ilustrován na následujícím obrázku pro dvě různé hodnoty K0NC a několik hodnot úhlu vnitřního tření φ pro pevně zvolené hodnoty parametrů κ*, λ*, ν. Je zřejmé, že kombinace M(K0NC = 0.6) = 0.774 a φ = 40° tyto podmínky nesplňuje, neboť první z výše uvedených výrazů dává hodnotu φmax = 33.2° < φ = 40°, zatímco v případě druhé podmínky dokonce dostáváme φmax = 32.8°, viz zelená varianta na obrázku (b).
Vzhledem k závislosti průmětu obou ploch plasticity do meridiální roviny na Lodeovu úhlu jsou obrázky prezentované pro případ triaxiálové komprese. Podrobnosti týkající se predikce změkčení Zobecněným Cam-clay modelem lze nalézt v popisu modelu, viz také porovnání odezvy Modifikovaného Cam-clay a Zobecněného Cam-clay modelu dostupné zde. Další podrobnosti jsou uvedeny v teoretické příručce.
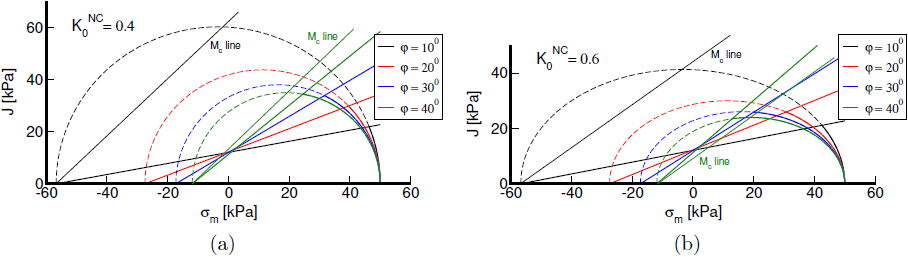 Tlaková a smyková podmínka plasticity: φ a K0NC: a) K0NC =0.4, b) K0NC =0.6
Tlaková a smyková podmínka plasticity: φ a K0NC: a) K0NC =0.4, b) K0NC =0.6
Vývoj překonsolidačního napětí pc, stejně tak význam parametrů definujících základní konstitutivní vztahy týkající se tlakové podmínky plasticity, je podrobně popsán v rámci popisu Modifikovaného Cam-clay modelu. Funkce plastického potenciálu, která řídí vývoj plastických přetvoření v oblasti smykového porušení, je totožná s plastickým potenciálem Drucker-Pragerova modelu. Je tudíž nezávislá na Lodeovu úhlu. Je tedy závislá pouze na hodnotě úhlu dilatance ψ (Mψ = Mψ(ψ)). Obecně platí, že φ ≠ ψ, což odpovídá neasociovanému zákonu plastického tečení. Podobně jako v případě Drucker-Pragerova modelu lze dilatanci (vývoj kladných objemových plastických přetvoření během plastického smýkání) omezit zavedením maximálního čísla pórovitosti emax, pro které předpokládáme dosažení kritického stavu, tedy ψ = 0.
Parametry definující Soft soil materiálový model jsou shrnuty v následující tabulce.
Symbol | Jednotky | Popis | |
|
| Směrnice linie bobtnání | |
|
| Směrnice linie normální izotropní konsolidace | |
|
| Maximální číslo pórovitosti na diagramu | |
|
| Poissonovo číslo | |
| [kPa] | Efektivní součinitel koheze | |
|
| Efektivní úhel vnitřního tření | |
|
| Úhel dilatance | |
| [kN/m3] | Objemová tíha | |
|
| Součinitel příčného tlaku v klidu normálně konsolidované zeminy | |
|
| Maximální číslo pórovitosti pro ukončení dilatance (při omezení dilatance) | |
|
| Součinitel překonsolidace | |
| [kPa] | Součinitel předchozího přetížení (preoverburden pressure) | |
| [1/K] | Součinitel teplotní roztažnosti (při uvažování teploty) | |
|
| Úhel vnitřního tření příslušný kritickému stavu (nezadává se) | |
| [kPa] | Překonsolidační napětí |
Podobně jako v případě Modifikovaného Cam-clay modelu se přímo nezadává modul pružnosti. Tento parametr se vyjadřuje z objemového modulu Ks vyjádřeného vztahem
![]()
Vývoj tuhosti je stejně jako u Modifikovaného Cam-clay modelu závislý na středním efektivním napětí σm. Nastavení počátečních hodnot překonsolidačního napětí pcin, objemového modulu Ksin, a počátečního čísla pórovitosti ein je podrobně popsáno v rámci popisu Modifikovaného Cam-clay modelu. S tím souvisí také volba počátečního výpočtového kroku, kdy při velmi malých hodnotách napětí je nutné volit tento krok dostatečně malý. Pro urychlení konvergence je možné s výhodou využít parametr nastavení výpočtu Minimální počet iterací pro jeden výpočetní krok. Vliv počáteční délky kroku na predikovaný vývoj napětí a přetvoření je podrobně popsán zde.
Na rozdíl od ostatních modelů Mohr-Coulombova typu se počáteční číslo pórovitosti ein, které odpovídá stavu zeminy na konci první výpočetní fáze (geostatická napjatost), nezadává, ale ale počítá ze zadané hodnoty čísla pórovitosti e0 a aktualního stavu napětí, viz také popis Modifikovaného Cam-clay modelu.
Model umožňuje upravit počáteční hodnotu parametru pc v závislosti na předpokládaném stupni překonsolidace pomocí parametrů ![]() a
a ![]() . Podrobnosti jsou uvedeny zde. Poznamenejme, že tento krok je umožněn pouze v případě, kdy počáteční napjatost je stanovena pomocí K0 procedury.
. Podrobnosti jsou uvedeny zde. Poznamenejme, že tento krok je umožněn pouze v případě, kdy počáteční napjatost je stanovena pomocí K0 procedury.
V případě výpočtu za předpokladu neodvodněných podmínek lze použít pouze variantu 1: Typ úlohy (1): výpočet v efektivních napětích (cef, φef).
Soft soil model umožňuje řešit také úlohu stability. Tato možnost je však dostupná pouze v případě, kdy úloha stability je řešena v rámci příslušné fáze budování. Úloha je řešena postupnou redukcí parametrů smykové pevnosti c, φ tak, jak je vysvětleno např. v popisu Drucker-Pragerova modelu. V tomto případě se uplatní pouze smyková podmínka plasticity. Tlaková podmínka plasticity je vypnuta.
Chování modelu v rámci jednoduchých laboratorních testů je ilustrováno zde včetně porovnání s Modifikovaným Cam-clay modelem a vlivu volby počátečního výpočtového kroku.
Podrobná implementace Soft soil modelu do programu GEO5 MKP je popsaná v teoretické příručce.
Literatura:
[1] R.B.J. Brinkgreve, Geomaterial Models and Numerical Analysis of Softening, PhD thesis, Technische Universiteit Delft, 1994. Available at https://repository.tudelft.nl/record/uuid:6738de62-4dde-45b0-b3bd-3635504767c2.