Online nápověda

Model hipoplastyczny dla iłów

Model hipoplastyczny glin (iłów) ma zastosowanie w modelowaniu drobnoziarnistych gruntów miękkich. Podobnie jak wszystkie inne modele należy on do rodziny standardowych modeli fenomenologicznych. Jako model określający reakcje gruntu zalicza się go do modeli stanów krytycznych. (Cam Clay, Uogólniony Cam Clay). Model ten jednakże uwzględnia nieliniową reakcję gruntu zarówno przy obciążaniu, jak i odciążaniu. W porównaniu do innych modeli opartych na teorii plastyczności, pozwala on na wyliczenie tylko całkowitych odkształceń. Tak więc nie ma w nim rozróżnienia między odkształceniami sprężystymi i plastycznymi. Wskazania rodzaju i umiejscowienia potencjalnych uszkodzeń (deformacji) gruntu, podawane w innych modelach w postaci ekwiwalentnych dewiatorycznych odkształceń plastycznych, w modelu hipoplastycznym mogą być przedstawiane poprzez rozkład aktywnego kąta tarcia wewnętrznego.

Przy określaniu reakcji gruntu, model ten pozwala na odzwierciedlenie różnych sztywności w obciążaniu i odciążaniu, osłabianiu, lub wzmacnianiu, w zależności od zagęszczenia gruntu i zmianie objętości przy ścinaniu (rozszerzanie, kompresja). Rzeczywista sztywność zależy nie tylko od kierunku obciążania, ale również od stanu gruntu wyrażanego jego porowatością. Inaczej niż w modelach Cam Clay, model ten całkowicie wyklucza naprężenia rozciągające w gruncie - zobacz rysunek 1a.

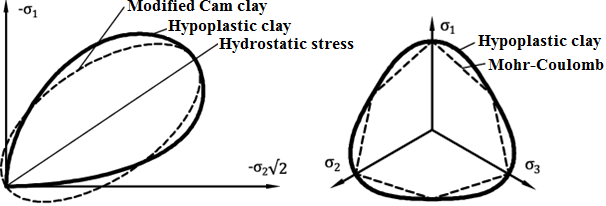Rysunek 1: Stan brzegowy modelu hipoplastycznego - (a) w porównaniu do powierzchni plastyczności w modelu Cam Clay, w płaszczyźnie południkowej; (b) w porównaniu do powierzchni plastyczności w modelu Mohr-Coulomb'a, w płaszczyźnie dewiatorowej

W przypadku modelu hipoplastycznego standardowa powierzchnia plastyczności zamieniona jest przez tzw. powierzchnię stanu brzegowego. Jej rzut na płaszczyznę dewiatorową jest podobny jak dla modelu z rysunku 1.b. Niestowarzyszone prawo płynięcia powoduje tworzenie niesymetrycznej macierzy sztywności (proszę porównać np. z modelem Mohr-Coulomb gdy mamy różne wartości dla kąta tarcia wewnętrznego φ i kąta dylatancji ψ). Szczegóły odnośnie opracowania modelu można znaleźć w [1].

Parametry modelu

Podstawowa wersja modelu wymaga określenia 5. parametrów materiałowych:

• Kąt tarcia wewnętrznego dla stałej objętości (kąt krytyczny tarcia wewnętrznego) φ_cv
• Nachylenie linii pęcznienia κ*
• Nachylenie normalnej linii konsolidacji (NCL - normalna linia konsolidacji) λ*
• Początek normalnej linii konsolidacji N
• Stosunek modułów odkształcenia objętościowego i ścinania r

Parametry κ*, λ* oraz N wyznaczają bilinearny (dwuliniowy) wykres konsolidacji izotropowej w skali logarytmicznej - rysunek 2a. Jeśli dostępne są parametry bilinearnego modelu Cam Clay (skala półlogarytmiczna, rysunek 2b), możliwe jest wprowadzenie tych wartości, na podstawie których zostaną wyznaczone na podstawie analizy wstecz parametry modelu hipoplastycznego. Parametrami bilinearnego modelu Cam Clay są:

• Nachylenie linii pęcznienia κ (w skali półlogarytmicznej)
• Nachylenie normalnej linii konsolidacji λ (w skali półlogarytmicznej)
• Wskaźnik porowatości e_max dla normalnej konsolidacji izotropowej przy ciśnieniu 1kPa

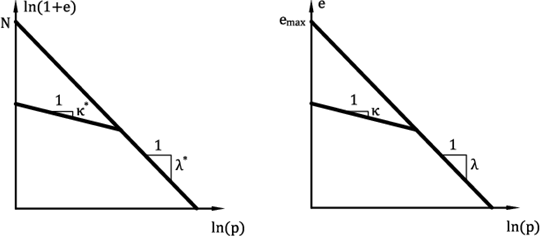Rysunek 2: Wykres bilinearny konsolidacji izotropowej - (a) Model Hipoplastyczny, (b) Model Cam clay

Kąt krytyczny tarcia wewnętrznego φ_cv

• Identyczny zarówno dla próbki oryginalnej (NNS), jak i próbki odtworzonej, a następnie prekonsolidowanej
• Można wyznaczyć na podstawie standardowego badania trójosiowego, stosując różne ciśnienia komorowe na odtworzoną próbkę
• Można wykonać badanie dla warunków z drenażem i bez drenażu (szybszy)
• Zwykle wartości tego parametru mieszczą się w zakresie 18° - 35°

Nachylenie normalnej linii konsolidacji λ*

• Wyznaczane graficznie z krzywej obciążenia w badaniu edometrycznym lub w badaniu konsolidacji izotropowej - zobacz rysunek 3
• Dla glin (iłów) zwięzłych preferowane jest wykonanie badania na próbce odtworzonej
• Zwykle wartości tego parametru mieszczą się w zakresie 0.04 - 0.15

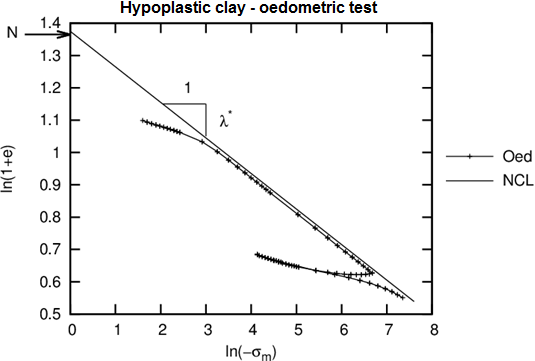Rysunek 3: Przebieg symulacji badania edometrycznego z modelem hipoplastycznym

Nachylenie linii pęcznienia κ*

• Może być wyznaczone podobnie jak dla parametru λ* - graficznie, lub poprzez wykonanie badania parametrycznego - poprzez porównanie pomiarów i symulacji po krzywej odciążania w badaniu konsolidacji edometrycznej, lub izotropowej - zobacz rysunek 3
• Zwykle wartości parametru κ mieszczą się w zakresie 0.01 - 0.02
• Wskaźnik (stosunek) λ/κ powinien być większy niż 4.0

Początek normalnej linii konsolidacji N

• Wyznaczany jest graficznie z krzywej obciążania w badaniu konsolidacji edometrycznej, lub izotropowej
• Test należy przeprowadzać na próbce nienaruszonej - gdy szukane jest przecięcie linii "lambda" z osią pionową, możliwe jest wyznaczenie nachylenia "lambda" uzyskanego z próbki odtworzonej - zobacz rysunek 3.
• Zwykle wartości tego parametru mieszczą się w zakresie 0.8 - 1.6

Wskaźnik (stosunek) modułów odkształcenia objętościowego i ścinania r

• Fizyczne znaczenie tego parametru wyrażone jest wzorem r = K_i/G_i
• K_i odpowiada stycznemu modułowi odkształcenia objętościowego przy kompresji izotropowej, zgodnie z normalną linią konsolidacji.
• G_i odpowiada stycznemu modułowi ścinania z badania na ścinanie bez drenażu, przy założeniu takiego samego stanu naprężeń.
• Parametr r może być wyznaczony poprzez badania parametryczne w badaniu trójosiowego ścinania
• Zwykle wartości tego parametru mieszczą się w zakresie 0.05 - 0.7

Określanie początkowego stanu gruntu

W modelu hipoplastycznym rzeczywisty stan gruntu jest powiązany z rzeczywistą zagęszczeniem wyrażanym wskaźnikiem porowatości. Implementacja modelu pozwala na bezpośrednie zdefiniowanie wskaźnika porowatości, lub może to być on wyliczony na podstawie wprowadzonego wskaźnika prekonsolidacji OCR.W pierwszym przypadku wprowadzona wartość e₀ odpowiada wskaźnikowi porowatości mierzonemu na nieobciążonej próbce wydobytej z określonej głębokości - zobacz rysunek 4a. W drugim przypadku, definiowana jest wartość OCR. Parametr ten przedstawia stosunek między naprężeniem średnim na linii NCL i początkowym naprężeniem średnim - zobacz rysunek 4b.

Przy inicjalizacji zadania za pomocą proceduy K₀, stan naprężeń początkowych odpowiada stanowi z końca tego etapu obliczeń. Jeśli wyliczenia rozpoczniemy od zerowego naprężenia początkowego (model hipoplastyczny jest już wprowadzony w pierwszym etapie obliczeń), przyjmuje się, że wartość naprężenia początkowego p_in = 1 kPa i utrzymuje się e_curr = e₀. Pod warunkiem, że inny materiał (uwzględniony na przykład w pierwszym etapie obliczeń) zostanie zamieniony przez model hipoplastyczny (np. w drugim etapie), przyjmowany jest początkowy stan naprężeń z poprzedniego etapu obliczeń.

Należy przypomnieć, że przy zastosowaniu modelu sprężystego, w pierwszej fazie obliczeń, wynikowy stan naprężeń odpowiada wynikom osiągniętym z zastosowaniem procedury K_o dla K_o (gdzie ν jest wsp. Poissona).

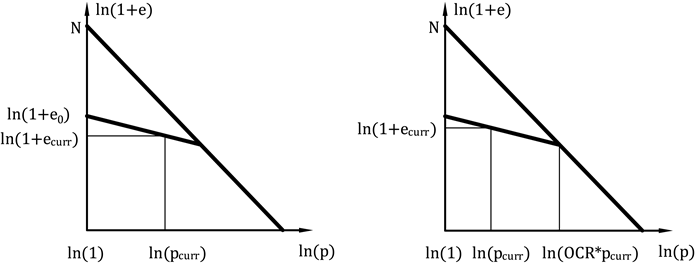Rysunek 4: Inicjalizacja wskaźnika porowatości - (a) bezpośrednie wprowadzenie początkowego wskaźnika porowatości, (b) inicjalizacja poprzez OCR

Z rysunku 5 widać, że dla normalnie skonsolidowanych gruntów, stan, dla którego OCR = 1.0 odpowiada tylko konsolidacji izotropowej, dlatego również K_o = 1.0. Jeśli grunt znajduje się w niezerowym stanie naprężenia dewiatorowego odpowiadający OCR dla normalnie skonsolidowanych gruntów jest większy od 1.0. Dokładna wartość zależy zarówno od parametów gruntu jak i ścieżki naprężenia (wartość K_o). Rysunek 5 pokazuje zależność minimów dla róznych wartości K_o i różnych rodzajów gruntów spoistych. Konkretne wartości podano również w Tablicy 1. Podstawowe parametry materiałowe tego zestawu gruntów podano w Tablicy 2.

Wybór OCR = 1.0 dla gruntów normalnie skonsolidowanych oraz K_o różnego od 1.0 powoduje nieakceptowalny stan naprężeń, który może prowadzić do braku konwergencji obliczeń.

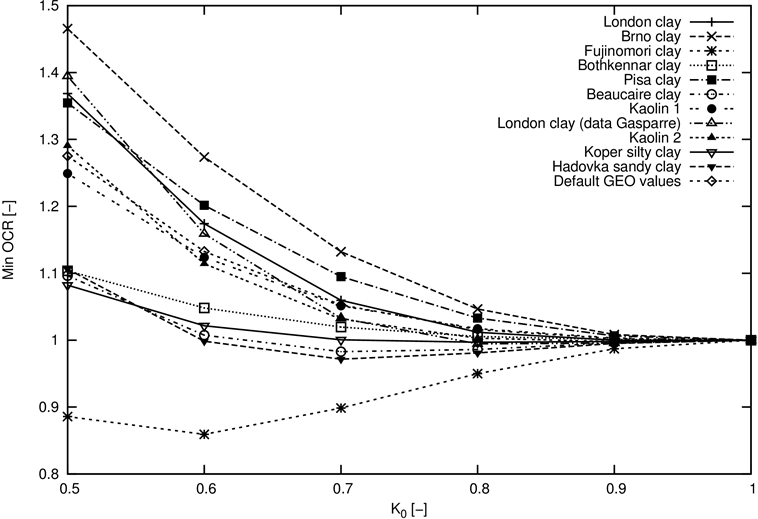Rysunek 5: Zależność OCR od współczynnika parcia spoczynkowego Ko

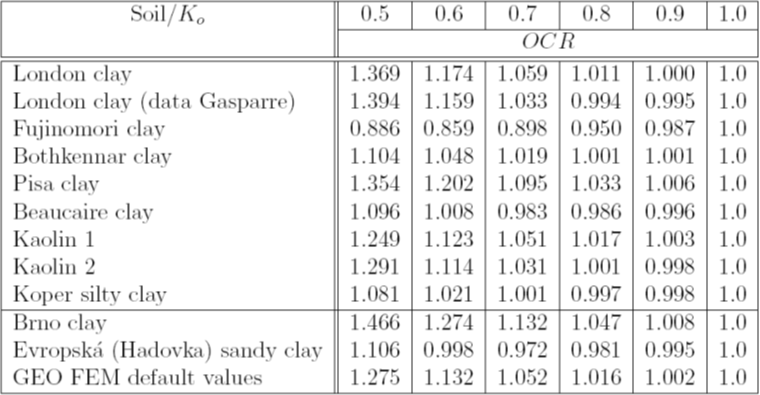Tabliza 1: Wskaźnik prekonsolidacji OCR dla wybranych gruntów w funkcji wartości Ko

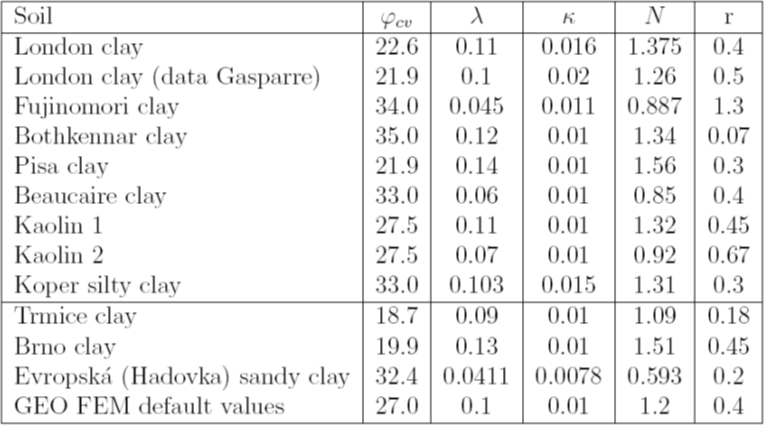Tablica 2: Parametry materiałowe wybranych gruntów

Odkształcenia międzyziarnowe

Podstawowa wersja modelu jest odpowiednia dla analiz z przeważającym kierunkiem ścieżki naprężeń. W przypadku obciążeń cyklicznych (obciążanie - odciążanie - ponowne obciążanie) bardziej odpowiednie jest stosowanie zaawansowanych formuł z zastosowaniem koncepcji odkształceń międzyziarnowych. Pozwala to na ograniczenie nieakceptowanego wzrostu deformacji stałych powstających podczas małych powtarzających się zmianach obciążenia (typu "zapadkowego"). Wprowadzenie odkształceń międzyziarnowych pozwala na modelowanie dużych sztywności, charakterystycznych dla gliny (iłu) w zakresie małych odkształceń. Opcja ta nie wchodzi do żadnych innych modeli zastosowanych w programie GEO5 MES. Koncepcja odkształceń międzyziarnowychh zakłada, że całkowita deformacja gruntu składa się z małych deformacji warstw międzyziarnowych (odkształceń międzyziarnowych), oraz deformacji powodowanych przez wzajemne przesuwanie się ziaren. Zmiana ścieżki obciążenia powoduje najpierw zmianę odkształcenia międzyziarnowego. Po osiągnięciu wartości granicznej odkształcenia międzyziarnowego, ustalona zostaje deformacja powiązana z ruchem ziaren.

Stosowanie koncepcji odkształceń międzyziarnowych wymaga zdefiniowania dodatkowych pięciu parametrów:

• Zakresu elastycznego odkształcenia międzyziarnowego R
• Parametrów m_R oraz m_T kontrolujących sztywność małych odkształceń
• Parametrów β_r oraz χ kontrolujących stopień degradacji sztywności przy wzroście odkształceń ścinających.

Parametry te są kalibrowane na podstawie znanych już danych materiałowych podstawowego modelu hipoplastycznego.

Margines sprężystej deformacji międzyziarnowej R

• Wyznacza zakres maksymalnego odkształcenia międzyziarnowego
• Może być wyznaczony na podstawie badań parametrycznych krzywej degradacji G = G(ε_s), Rysunek 5
• Zamiennie może być uwzględniony jako stała niezależna od materiału R = 10^-4
• Zwykle wartości tego parametru mieszczą się w zakresie 2_*10^-5 - 1_*10^-4

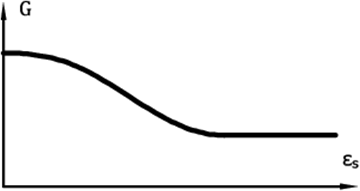Rysunek 6: Krzywa pokazująca utratę sztywności modułu ścinania

Parametr m_R

• Wyznacza wielkość modułu ścinania przy zmianie ścieżki obciążenia w płaszczyźnie południkowej (σ_m - J) o 180°
• Zależność liniowa między parametrem m_R i początkowym modułem ścinania G₀ uzyskiwana jest z wyrażenia G₀ = p_*(m_r/(r_* λ*)
• Początkowy moduł ścinania może być wyznaczony z pomiaru propagacji fal ścinania [2]
• Zwykle wartości tego parametru mieszczą się w zakresie 4.0 - 20.0

Parametr m_T

• Wyznacza wielkość modułu ścinania przy zmianie ścieżki obciążenia w płaszczyźnie południkowej (σ_m - J) o 90°
• m_R/m_T = G₀/G₉₀
• Wskaźnik (stosunek) modułów początkowych można oszacować na podstawie wskaźnika tych modułów dla dużych odkształceń.Wartość stosunku m_R/m_T zwykle mieści się w zakresie 1.0 - 2.0
• Zwykle wartości parametru m_T mieszczą się w zakresie 2.0 - 20.0

Parametry β_r oraz χ

• Wyznaczają szybkość degradacji sztywności przy wzrastającym odkształceniu ścinającym
• Mogą być wyznaczone poprzez badania parametryczne krzywej degradacji G = G(ε_s)
• Zwykle wartości parametru β_r mieszczą się w zakresie 0.05 - 0.5
• Zwykle wartości parametru χ mieszczą się w zakresie 0.5 - 6

Literatura:

[1] D. Mašín, A hypoplastic constitutive model for clays, International Journal for Numerical and Analytical Methods in Geomechanics., 29:311-336, 2005.