Depth of Deformation Zone
The assumed depth of influence is a variable, which considerably influences the stiffness of soil below the pile heel. It is one of the input parameters for the determination of parameters C1 and C2 of the Winkler-Pasternak model. The deeper the influence zone the smaller the stiffness of subsoil. When the depth of influence zone approaches in the limit zero the stiffness of subsoil tends to infinity.
The depth of influence zone depends both on subsoil parameters and magnitude of the applied surcharge, thus on stress below the pile heel. The program assumes that the depth of the influence zone is found in the location, where the stress below the heel equals the geostatic stress. Such an idea is depicted in the following figure:
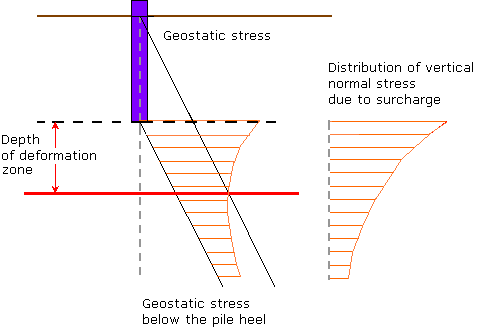 Determination of the depth of influence zone below the pile heel
Determination of the depth of influence zone below the pile heel
For digital determination of the depth of influence zone H serves the function F(β). Its distribution appears in the figure. This function was derived using the above assumptions and in the program appears in the form of a table. Its application is evident from the following steps. The values of F(β) are determined for the current value of stress fz below the pile heel and for the original geostatic stress γh. For this value of F(β) we determine the parameter β. This value serves to determine for the actual value Poisson's ratio ν and pile diameter r the corresponding depth of influence zone H.
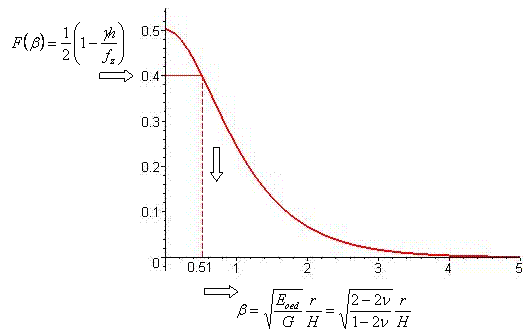 Variation of function F(β)
Variation of function F(β)
The depth of influence zone can be affected by the presence of groundwater. In such s case its determination is outlined in the following figure:
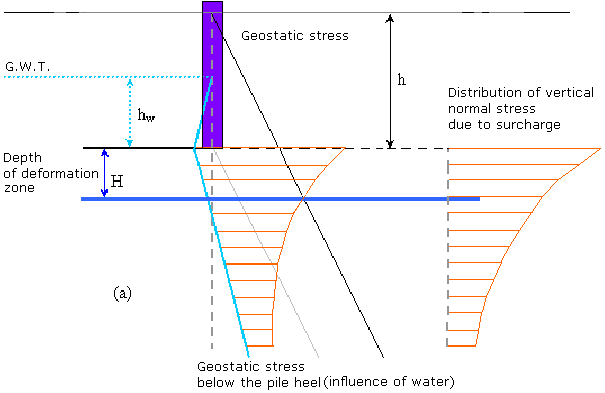 Determination of the depth of influence zone below the pile heel including water
Determination of the depth of influence zone below the pile heel including water
For digital determination of the depth of influence zone H is then used the function G(β). Its distribution appears in the figure. In the analysis this function is exploited in a similar way as function F(β). The only difference when determining the values of G(β) appears in the use of hydrostatic pressure γw*hw.
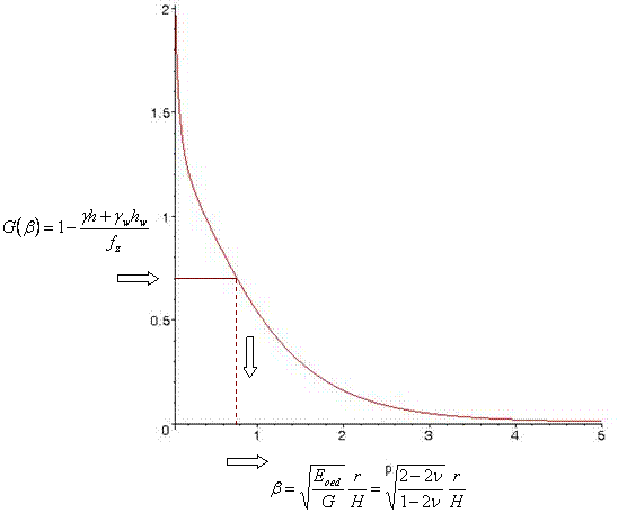 Variation of function G(β)
Variation of function G(β)