Solution Procedure
The principle of calculation of rock slope stability for polygonal slip surface is shown in the following figures.
 Rock Slope Scheme
Rock Slope Scheme
The stability analysis is conducted in a sequential manner for all blocks ranging from the uppermost block to the lowest block. The stability of each block is assessed to the required factor of safety and forces acting on the next (lower) block are calculated. The lowest calculated value of stability from all blocks is given as the final stability of the rock slope.
Di is the vector representing the resultant of all the disturbing forces acting on the block i given by:
![]()
where: | Wi | - | weight of the block |
Pi | - | external forces (loads) acting on the block | |
Ei | - | earthquake forces on the block | |
Ui | - | force due to water on external slip surface | |
Vi | - | force due to water on internal slip surface | |
Hi | - | force due to water above the terrain | |
Bi | - | anchor force on the block |
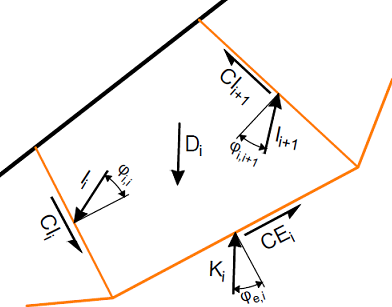 Forces acting on block
Forces acting on block
where: | D | - | resultant of all external forces acting on the block |
CI | - | cohesion on internal slip surface | |
CE | - | cohesion on external slip surface | |
I | - | interaction force | |
K | - | reaction force on external slip surface |
To assess the stability of the block i the resultant force R is determined. It consists of resultant of external forces D and forces acting on the block from the previous block:
![]()
If the tensile has occurred on the external slip surface, the stability of the block against slip on the internal slip surface is assessed.
![]()
![]()
where: | Ti | - | resisting force |
φi | - | angle of the internal friction on the internal slip surface | |
RN,i | - | normal component of R | |
RT,i | - | tangential component of R | |
CIi | - | cohesion on internal slip surface |
If the external slip surface is loaded by compression, the factor of safety FS, for which the equilibrium of forces acting on the block is fulfilled, is determined. The force R, cohesion on internal and external slip surface must be in equlibrium with the reaction K and interaction force I. The inclination of forces K and I is given by φM.
![]()
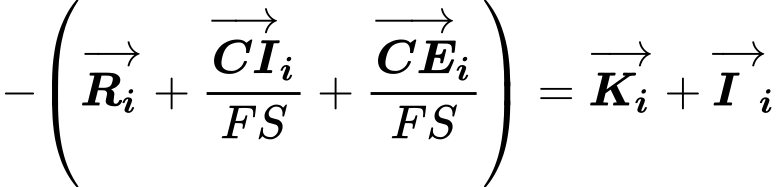
The resulting value of SF, when the equilibrium on the block is fulfilled, is compared with the required factor of safety.